| Dessins |
Jeux |
Exos |
Autres |
Dessins
Des programmes qui dessinent des schémas basés sur des règles toutes simples.
En faisant varier les couleurs, on obtient des résultats super jolis !
Cliquer sur les images pour accéder aux programmes (nouvel onglet).
Cliquer sur les sources pour les explications détaillées.
En faisant varier les couleurs, on obtient des résultats super jolis !
Cliquer sur les images pour accéder aux programmes (nouvel onglet).
Cliquer sur les sources pour les explications détaillées.
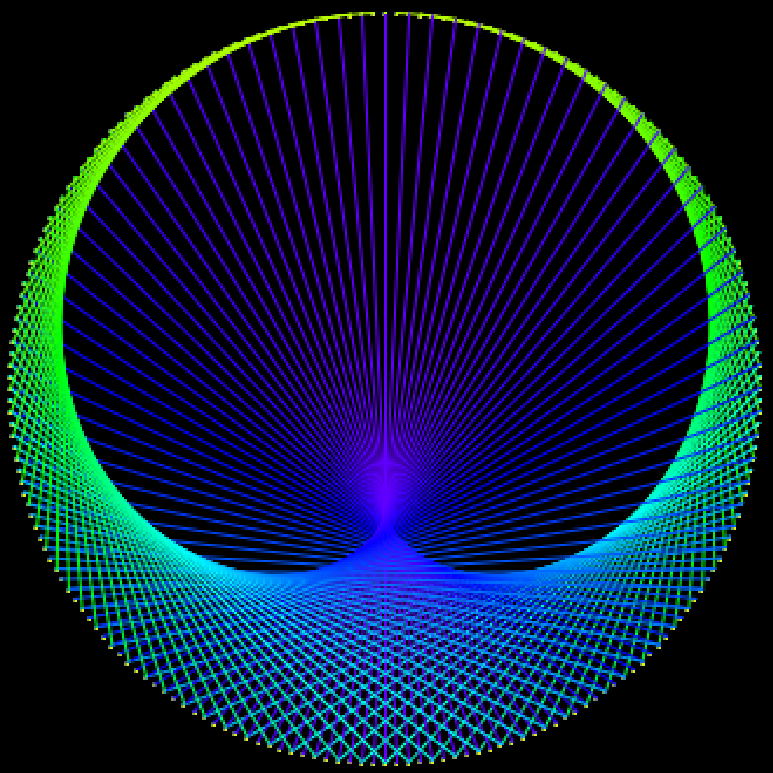 |
Des rosaces apparaissent dans les tables de multiplication. On dessine des points sur un cercle, on les numérote 0, 1, 2, 3... en partant de celui d'en haut, et on trace un segment entre un point et son multiple. Pour tracer la table de 2, 1 est relié à 2 ; 2 est relié à 4 ; 3 est relié à 6 ; etc. Le programme peut tracer les segments dans l'ordre, ou par boucle. On peut colorier les boucles, les segments indépendamment ou en fonction de la taille. Source Source 2 |
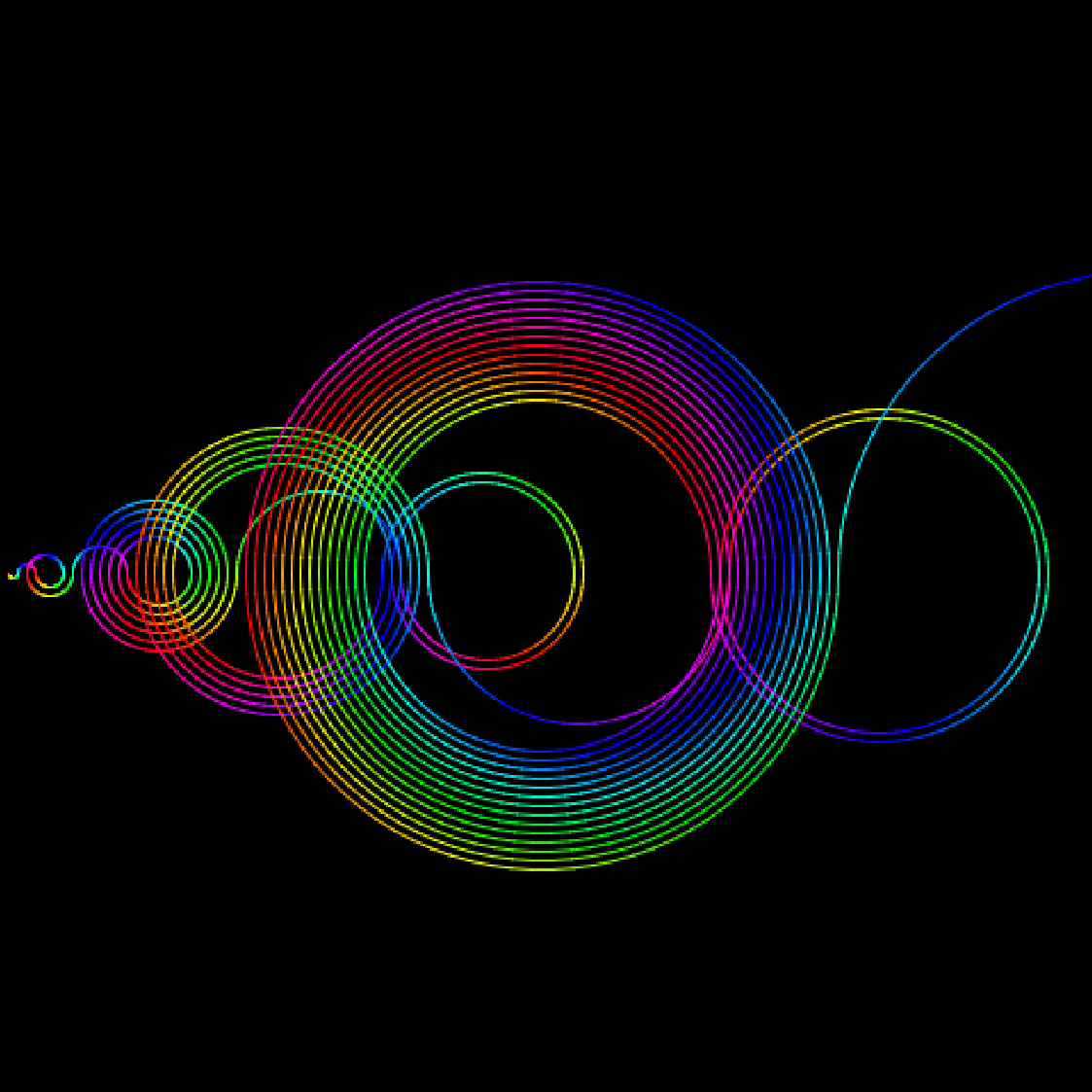 |
La suite de Recaman On avance sur une demi-droite graduée en traçant des demi-cercles de diamètres 1, 2, 3... On trace les demi-cerles une fois au-dessus de la demi-droite et une fois en dessous. Si on peut revenir en arrière sur un point d'abscisse positive sur lequel on n'est pas déjà passé, on y va. Sinon, on continue à avancer. Source |
 |
Automate cellulaire On part avec une seule cellule coloriée sur la première ligne. On décide d'une règle qui dit si une cellule sera coloriée ou non sur la ligne suivante en fonction de son état actuel et de l'état de ses voisines. On laisse tourner sur plusieurs lignes. On obtient différents dessins en fonction de la règle qu'on a choisie. Source Source 2 |
 |
La courbe du dragon On plie une bande de papier en deux, et encore en deux, et encore... On déplie notre bande en laissant tous les angles en angles droits. On obtient cette fractale. Source Source 2 |
 |
On lance une boule de billard depuis un coin d'une table rectangulaire ou en forme de parallélogramme. La boule trace un trait sur deux (ou sur trois, ou sur quatre...) et s'arrête lorsqu'elle atteint un autre angle. Source Source 2 |
 |
Cascade hexagonale On part avec une ligne sur laquelle il y a des cellules colorées. On construit la ligne en dessous, cellule par cellule, avec les règles suivantes : - Si les deux cellules au-dessus sont de couleurs différentes, on colorie de la 3e couleur. - Sinon, on colorie de la même couleur. Les règles à deux couleurs différent un peu mais c'est le même principe. On obtient différents dessins en fonction des cellules qu'on colorie sur la première ligne. Source |
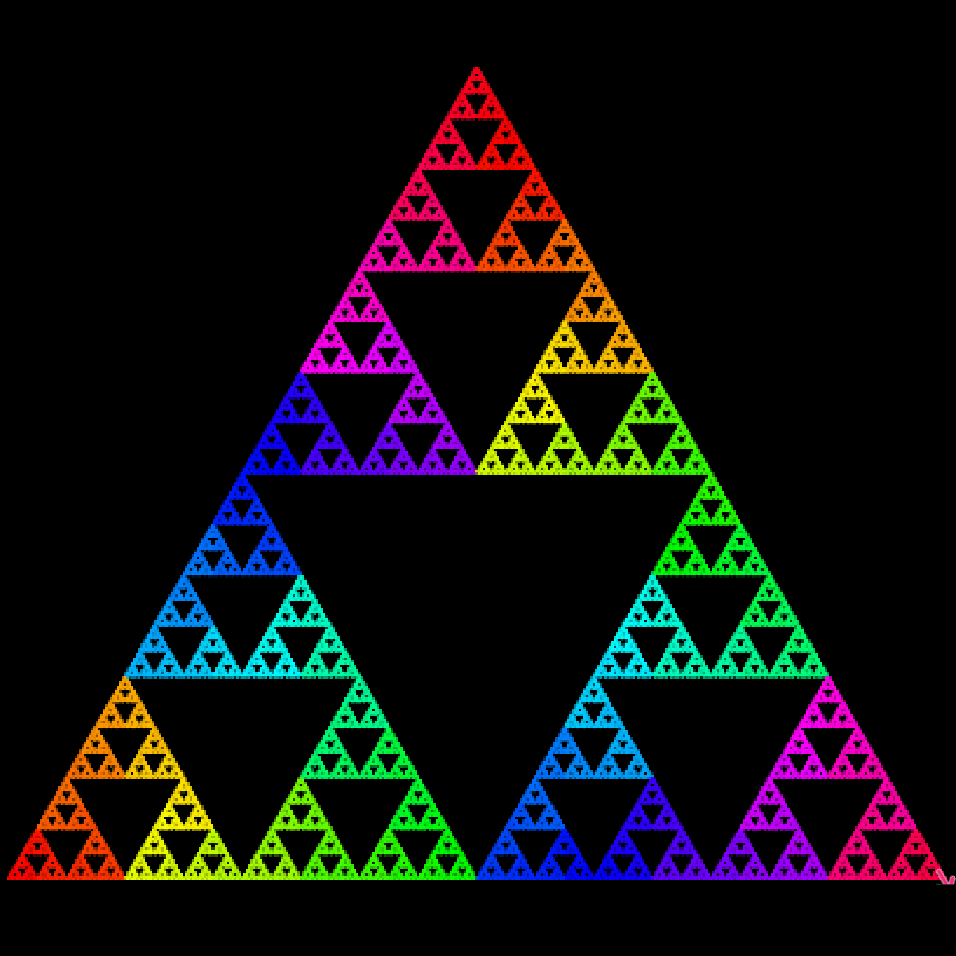 |
Le triangle de Sierpinski On trace un segment. On relie les extrémités de ce segment par trois segments formant la moitié d'un hexagone régulier. On efface le segment de départ. On répète cette étape pour tous les segments obtenus en alternant l'orientation des demi-hexagones. On obtient cette fractale. Source |
 |
Nombres premiers entre eux
Les lignes et les colonnes sont numérotées 1, 2, 3,... de gauche à droite et de bas en haut. Un carré est colorié si et seulement si ses coordonnées sont des nombres premiers entre eux, c'est-à-dire, si ce sont des nombres qui n'ont aucun diviseur en commun (à part 1). |
 |
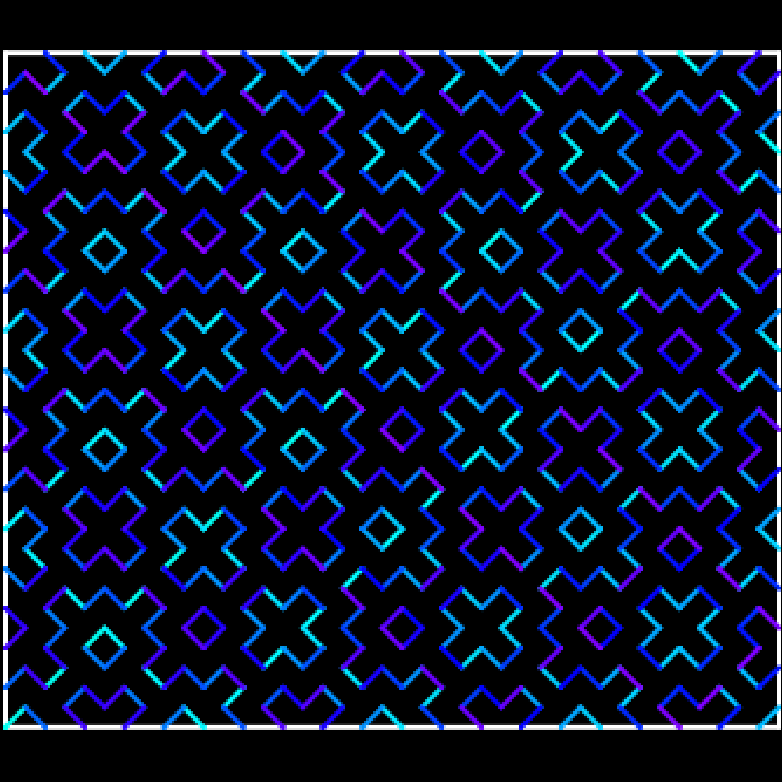
Hitomezashi Stitch Patterns Chaque ligne est construite de la même façon : un segment, un vide, un segment, un vide, etc. Certaines commencent par un segment et d'autres commencent par un vide. On peut laisser le programme décider, pour chaque ligne, par quoi elle va commencer aléatoirement, ou bien décider nous-mêmes. On peut aussi faire la même chose avec des lignes horizontales et verticales. Source |
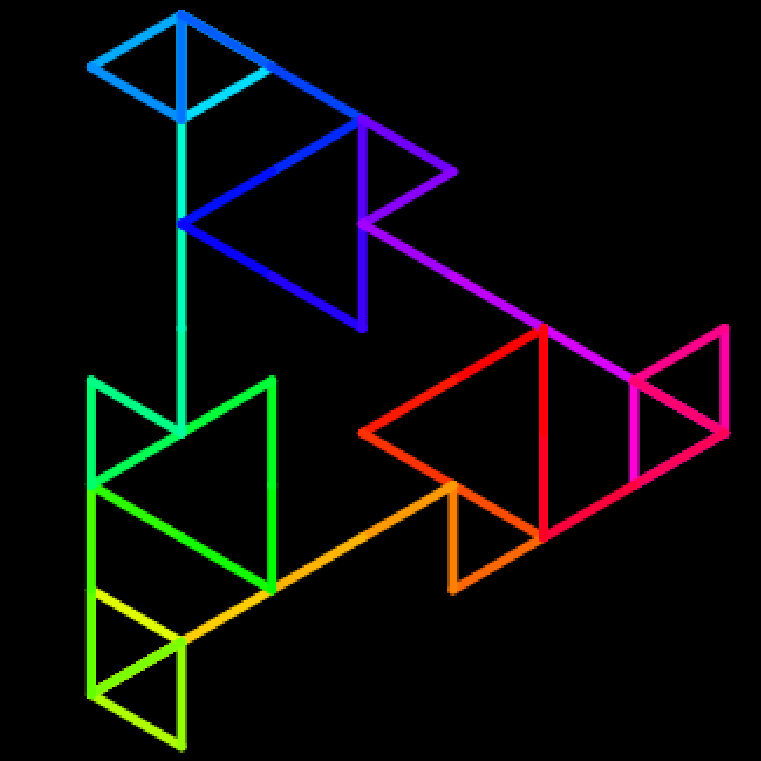 |
Étoiles rationnalles On fait une division et, pour chaque chiffre du quotient, on tourne d'une fraction de tour correspondant. Exemple : 1/7 = 0,142857142857... donc on tourne d'1 dixième de tour, puis de 4 dixièmes, puis de 2, de 8, etc jusqu'à revenir sur le point de départ. Si on compte en base 10, on a dix directions possibles mais si on compte en base 3, il n'y en a que 3 (comme sur l'image). On peut changer la division, la base, la taille, etc. Source |
 |
Thue-Morse sequence Une suite de 0 et de 1 construite d'une certaine façon. Quand on voit un 0, on se déplace d'un pas. Quand on voit un 1, on tourne de 60°. Pour des propriétés sympa sur la suite, voir mon programme Python ICI. Source |
 |
Mauer roses Les roses de Mauer. Voir les sources pour les explications. Source 1 Source 2 |
 |
Lindenmayer systems Les sytèmes de Lindenmayer. Voir les sources pour les explications. Source 1 Source 2 |
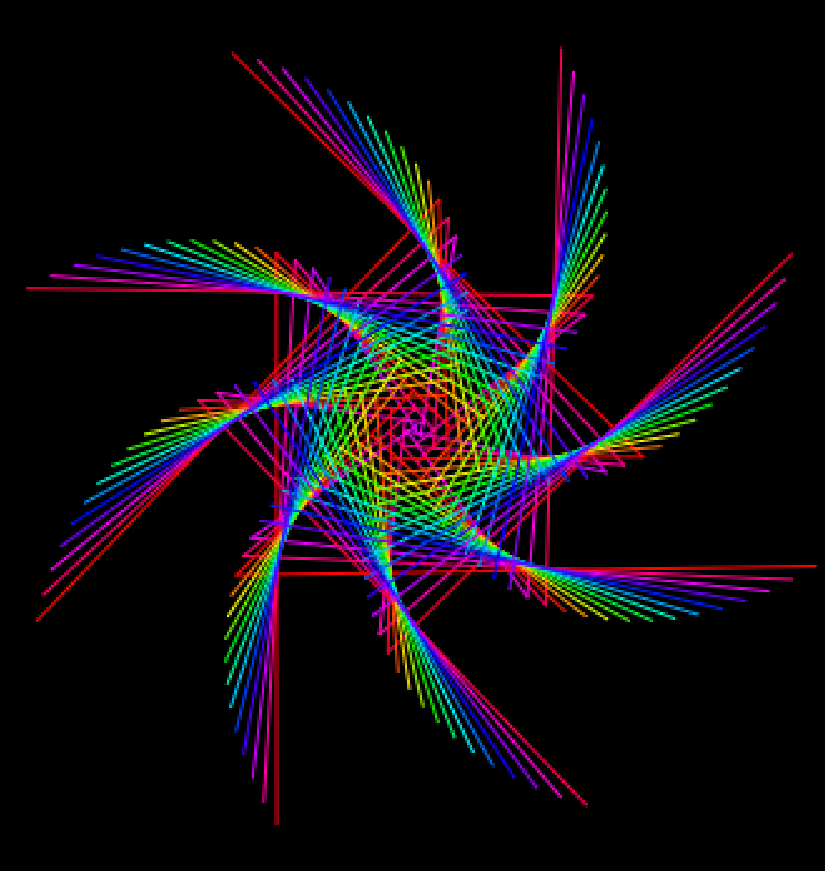 |
Spirales On crée une spirale de points. Ensuite, on relie les points numéros 1,1+j,1+2j,... avec une spirale puis 2,2+j,2+2j,... avec une autre puis 3,3+j,3+2j,... avec une autre, etc. Source |
 |
L'ensemble de Mandelbrot La superstar des fractales. Source Zoom |
Jeux Vidéo
Mes jeux vidéos.
| Quiz Géo Mon jeu le plus ambitieux : un quiz pour travailler la géographie. Pays : emplacements, capitales, drapeaux. États des États-Unis : emplacements, capitales. Départements français : emplacements, préfectures, numéros. Vous choisissez l'info donnée et l'info demandée. |
| Bubles battle Un petit jeu pour 2, 3 ou 4 joueurs. Chacun contrôle une petite bulle et doit tirer sur les autres joueurs en évitant leurs balles. On peut choisir plein de bonus, créer son niveau, le faire tourner, gérer le Mitrallator... |
| Flappy bat Comme Flappy bird (+ deux bonus et des ballons), mais avec une chauve-souris. |
| Ball jump Un jeu de réflexes où on doit sauter d'une plateforme à une autre, tout en invesant les plateformes si elles sont en haut et nous en bas ou inversement. |
| Course neige Une course à deux joueurs avec des turbos et des pièges sur une musique de Trans-Siberian Orchestra. |
| Jeux Noël Mon tout premier jeu. On se déplace de gauche à droite. Il faut prendre les cadeaux et les bonus et éviter les malus. |
Exercices
Je ne vais pas détailler jeu par jeu ici puisque le but de ce site est (entre autres) de remplacer ces jeux.
lien vers le studio
lien vers le studio
Autres
Programmes très variés, qui ont pris entre 1h et plusieurs jours à coder.
| Conversion bases Convertit en base n un nombre décimal donné en base 10 et inversement. |
| Décomposition en facteurs premiers Décompose un nombre donné en facteurs premiers. |
| Gaussienne Lance une pièce avec probabilité p, 1-p un certain nombre de fois. Affiche la gaussienne obtenue. |
| Paradoxe de Bertrand Illustre le paradoxe de Bertrand qui joue sur le fait que "prendre une corde d'un cercle au hasard" n'est, en fait, pas bien défini. Source |
| Killer orga Permet d'organier un killer. Le programme vous propose une cible parmi les joueurs inscrits, de sorte qu'il soit impossible de tuer quelqu'un qui nous avait pour cible (sauf quand il ne reste que deux joueurs, évidemment). |
| Overbooking Calcule l'espérance, pour les compagnies aériennes qui vendent plus de billets que de places disponibles, en fonction de tout un tas de paramètres. Source |
| Planche de Galton Simule une planche de Galton. Appuyer sur K pour afficher les commandes. |
| 4-card code Pour s'entraîner à un super tour de magie expliqué ici. |
| Jeu de la vie Le jeu de la vie, inventé et étudié par John Conway. Source |
| Labyrinthes Le programme qui m'a demandé le plus de temps, tout confondu. Dessiner n'importe quel labyrinthe, placer le départ et l'arrivée, l'algorithme trouvera la sortie, soit en utilisant l'algorithme de Trémeaux, soit celui de Dijkstra. Trémeaux Dijkstra |
| Poisson Un mini-jeu pour passer 5 min le 1er avril. |
| Mariages stables Chaque homme classe les femmes selon ses préférences. Chaque femme fait de même. L'algorithme trouve des couples stables (couples dans lesquels si une personne n'a pas son choix n°1 et est tentée d'être infidèle, la personne avec laquelle elle veut l'être n'est pas intéressée). Bien sûr, cet algorithme n'a jamais servi à créer des couples stables (enfin, j'espère) car le système est archaïque (mariages hétérosexuels et prédéfinis en fonction des goûts de chacun) mais il est utile sur Parcoursup si on remplace les hommes par des étudiants et les femmes par des écoles. Petite remarque : il peut exister plusieurs configurations stables. Le sexe qui propose est garanti d'avoir la meilleure alors que celui qui dispose aura la pire. Source |
| IA et allumettes À son tour, on prend 1, 2 ou 3 allumettes et celui prend la dernière a perdu. On joue contre un programme qui, au début, joue au hasard mais qui, quand il fait une erreur, l'efface de ses coups possibles. Si on joue avec 4n+1 allumettes, il devient imbattable au bout d'un certain temps. Inspiré de cette vidéo dans laquelle Matt Parker invente un système physique basé sur le même principe qui apprend de ses erreurs pour ne plus perdre au morpion. |
| Tarot Mon tout premier algorithme, fait sur AlgoBox à l'époque. C'est un programme qui compte les points au tarot : il n'y a qu'à répondre aux questions qu'il pose et il s'occupe de tout. |
| Jeu à somme non constante Chacun donne ce qu'il veut à la banque, la banque double le total et répartit le tout équitablement à tout le monde. Chaque joueur a intérêt à ne rien donner mais à ce que les autres donnent tout... |
| Enigma Gros projet ! Programme qui simule la machine Enigma que les Nazis utilisaient pour communiquer pendant la 2de guerre mondiale. Ce programme est plus complet que la machine (énormément de rotors, plus de cables sur le plugboard, plus de caractères) mais c'est le même principe. Source |